悪口として使われる「東大へ行け」
ドラマ「ドラゴン桜」の有名な台詞である「バカとブスこそ東大へ行け」という言葉は印象的ですね。X上でもこの言葉にちなんだ投稿が散見されます。悪口として使われえる
私はこの言葉を見るとき「バカまたはブスなのかな、バカかつブスなのかな」と感じます。
その度に、数学1の「命題と集合」を学習する題材として最適であるように感じるのです。
そこで今回は「バカとブスこそ東大へ行け」を題材に「命題と集合」を解説してみます。
命題とは
命題:真であるか偽であるかが明確に定まる主張
この記事は「バカとブスこそ東大へ行け」という言葉が真(正しい)か偽(間違っている)かを主張したいわけではありません。
さらに、厳密には「バカとブスこそ東大へ行け」は命題とは言えません。
ただ、この記事の趣旨は「バカとブスこそ東大へ行け」という言葉を題材に数学の論理を学ぶことですから、当記事では命題として扱います。
命題として扱う以上、真偽が明確に定まらなけらばいけませんが、「バカとブスこそ東大へ行け」という命題が真なのか偽であるかは、趣旨からずれるので、明言は避けさせていただきます。
複合命題
否定,論理和,論理積,含意によって複合命題が作られます。以下の説明でP,Qは命題だとします。
否定
¬P「Pでない」:Pが真であるとき¬Pは偽、Pが偽であるとき¬Pは真です。
論理和
P∨Q「PまたはQ」:Pが真のとき、Qが真のとき、PもQも真のときにP∨Qです。PもQも偽のときにP∨Qは偽です。
論理積
P∧Q「Pかつ」:PもQも真のときにのみP∧Qは真です。それ以外のときにはP∧Qは偽です。
含意
P⇒Q「PならばQ」:Pが真でQも真のときと、Pが偽のときにP∧Qは真です。Pが真でQが偽のときにのみP∧Qは偽です。Pが偽のときQの真偽にかかわらずP∧Qが真であることに注意が必要です。
「バカとブスこそ東大へいけ」という言葉を主語を補いながら複合命題の形にすると、
「あなたがバカとブスならば、あなたは東大へ行くべきだ」となります。
「あなたはブスとバカ」ならば「あなたは東大へ行くべき」
さらに言い換えると「『あなたがブス」または「あなたがバカ」』ならば「あなたは東大へ行くべき」となります。
どうして「バカとブスこそ東大へ行け」が命題でないのか
バカであるかとブスであるかは主観によるし、東大に行くべきかどうかも主観によるものです。主観によるものは真偽を明確に定めることができません。これが「バカとブスこそ東大へ行け」が命題として扱えない理由です。
命題として扱うために
バカかとブスかと東大に行くべきか、が明確に定まる物と仮定すると、「バカとブスこそ東大へ行け」が命題として扱えます。
注意するべきなのは、バカかとブスかと東大に行くべきか、が明確に定まる物と仮定しているだけだということです。バカかとブスかと東大に行くべきか、が明確に定まる物と私が主張しているわけではないです。
ド・モルガンの法則
論理和と論理積を含む命題を否定するときや、和集合や積集合の補集合を考えるときに成り立つ法則です。
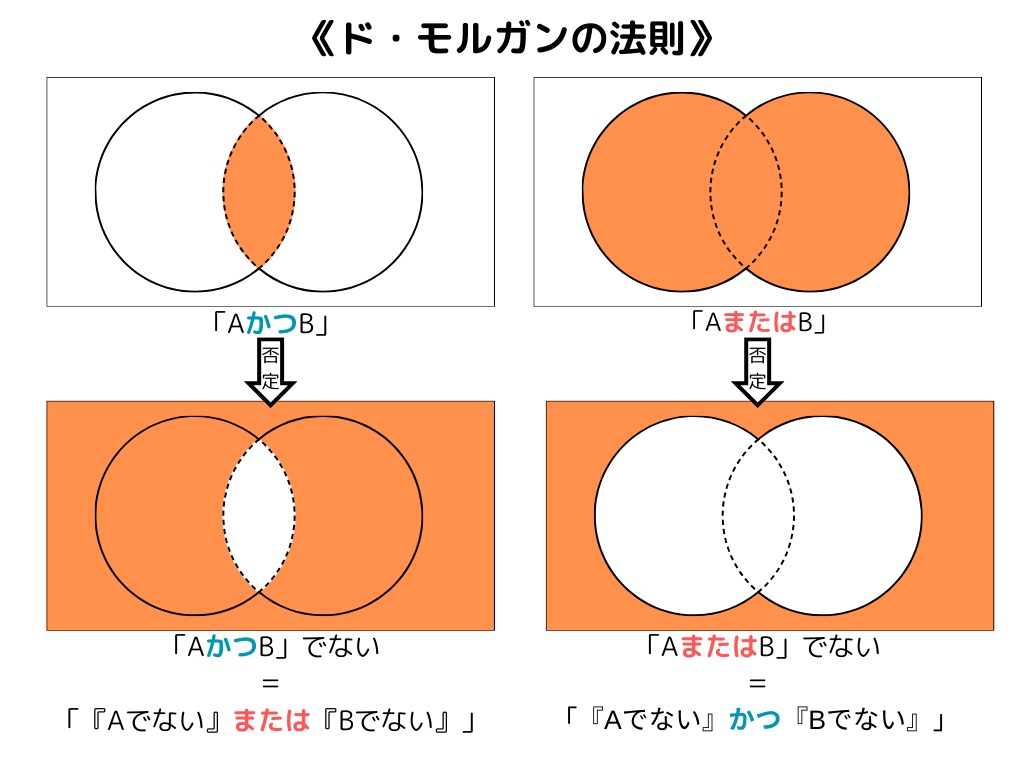
AかつBや、AまたはBを否定するときに、AとBが否定するだけではありません。またはとかつも否定によって変化します。
かつを否定するとまたはに変わり、またはを否定するとかつに変わります。
「バカとブス」の否定は?
「バカとブス」は「バカまたはブス」と言い換えることができます。
ド・モルガンの法則を使うと、「バカまたはブス」の否定は「バカでないかつブスでない」です。
「バカでない」=「賢い」、「ブスでない」=「美人」であるので、
「バカとブス」の否定は「賢いかつ美人」と言い換えられます。
「バカとブス」が「バカかつブス」と考えることはできないのか
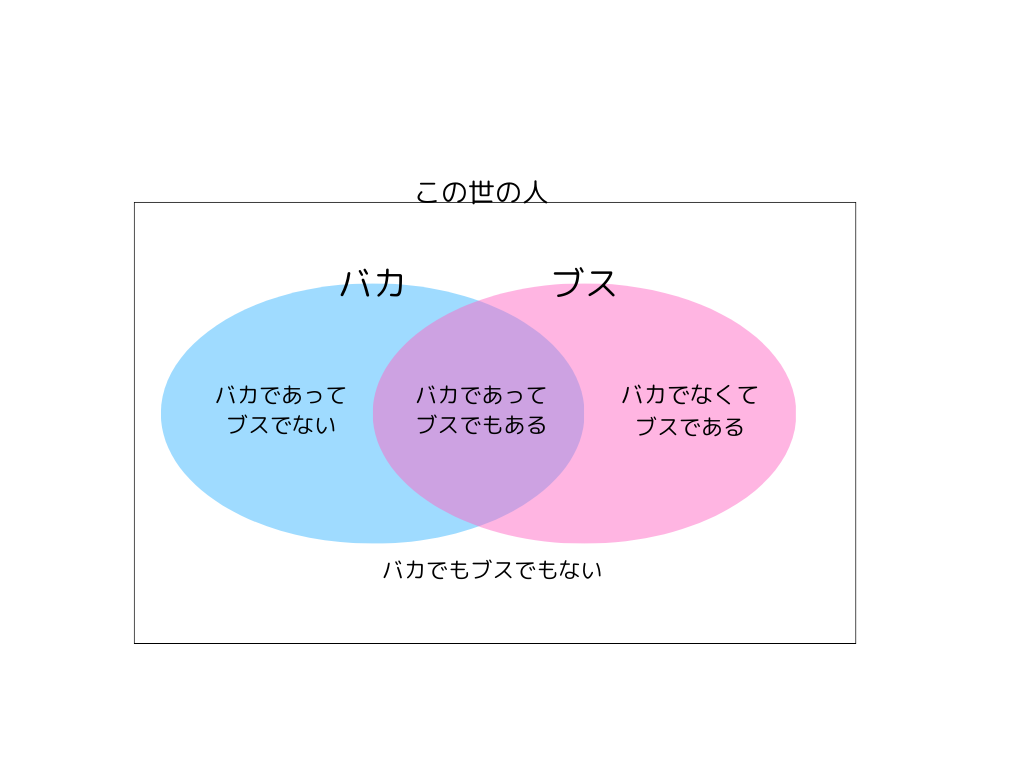
「バカとブス」が「バカかつブス」、つまり「バカでもあるしブスでもある」と考えられないことをドラマの文脈から確認します。
ドラマで「バカとブス」という言葉が出てくる流れを要約すると以下のようになります。
世の中の仕組みを知らないバカは、国に税金を払い続けさせられて搾取される。
国は税金を搾取し続けるためにバカはバカであり続けてほしい。
そんな状況の中で、搾取されたくなければ勉強するしかない。
つまり、搾取されるバカは勉強して搾取されなくなるべきだ、という意味だと考えられます。
この時、勉強をして東大に行くべきと言われいている「バカとブス」には全てのバカが含まれていると考えられます。
「バカかつブス」には全てのバカは含まれておらず、「バカまたはブス」には全てのバカが含まれています。
以上の理由から、「バカとブス」は「バカかつブス」でなく「バカまたはブス」の意味で解釈するべきです。
裏逆対偶
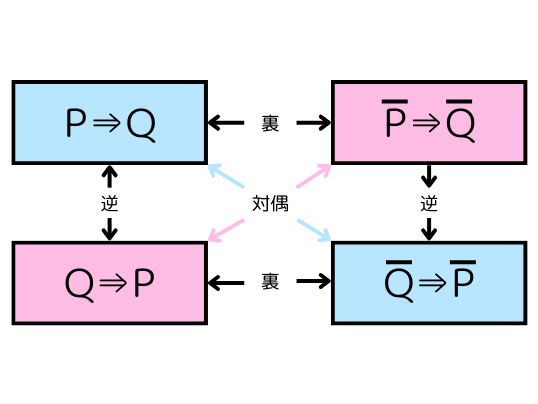
含意を含む命題についている名前です。Pに「バカまたはブスである」、Qに「東大に行くべき」を入れてみると以下のようになります。
元の命題 「バカまたはブスである」⇒「東大へ行くべき」
裏 「バカまたはブス」でない⇒「東大へ行くべき」でない
言い換えると、「賢いかつ美人」⇒「東大へ行くべきでない」
逆 「東大へ行くべき」⇒「バカまたはブス」
対偶 「東大へ行くべき」でない⇒「バカまたはブス」でない
言い換えると、「東大へ行くべきでない」⇒「賢いかつ美人」
対偶の命題の真偽は一致する
対偶の命題真偽は一致することは重要です。
ある命題を証明しにくいときにその命題の対偶を考えてみるという使い方をします。待遇を考えるとシンプルな命題になるということがあるからです。
「バカまたはブスである」⇒「東大へ行くべき」の真偽と、「東大へ行かないべき」⇒「賢いかつ美人」の真偽は一致します。
「バカまたはブスである」⇒「東大へ行くべき」が正しいか考えるとき、「東大へ行くべきでない」⇒「賢いかつ美人」について考えてみるのも同じことです。
東大へ行くべきでない人の中に、「賢いかつ美人」でない反例が一人でもいれば「東大へ行くべきでない」⇒「賢いかつ美人」が偽とな理、元の命題の「バカまたはブスである」⇒「東大へ行くべき」も偽であるとわかります。
賢いかつ美人な才色兼備な人がそう多くないことを考えると、東大へ行くべき人の中で反例を見つけるのは簡単かも知れません。
元の命題の裏と逆も対偶の関係
元の命題と対偶の真偽が一致するのと同じように、裏と逆の真偽も一致します。
これは、裏と逆が待遇の関係にあるからです。
注意しなければいけないのは、元の命題と対偶の真偽と裏と逆の真偽は一致しないということです。
仮に、元の命題と対偶が真だったからといって、裏と逆が真だとは言えないということです。
X上の「東大へ行け」は必ずしも悪意を含まないのでは?
X上で、東大へ行けとポストすることで、バカまたはブスであることを暗に言おうとするポストが散見されます。
こういったポストの背後に隠れているのは、「バカとブスこそ東大へ行け」の言い換えである「バカまたはブスである」⇒「東大へ行くべき」の逆の命題である「東大へ行くべき」⇒「バカまたはブス」が真であるという考えです。
元の命題の「バカまたはブスである」⇒「東大へ行くべき」が真なのかも知れないと考えるのは自由ですが、だったら逆の命題である「東大へ行くべき」⇒「バカまたはブス」も真だと思ってポストをしているのなら、愚かです。
阿部寛に言う通りに「バカまたはブスである」⇒「東大へ行くべき」が正しくても、それを根拠に「東大へ行くべき」⇒「バカまたはブス」が正しいと言うことはできません。
元の命題と逆の命題の真偽は必ずしも一致しないからです。
ここで、逆の命題である「東大へ行くべき」⇒「バカまたはブス」は真偽を考えてみましょう。
逆の命題である「東大へ行くべき」⇒「バカまたはブス」の対偶にあたる「賢いかつ美人」⇒「東大へ行くべきでない」という裏の命題の真偽を考えます。
「賢いかつ美人」な人の例として、東大ミスコンに出場する人や東大卒の美人アナウンサーを考えます。これらの人が「東大に行くべき」であれば、裏の命題の反例になりますね。
反例が一人でもいた時に、裏の命題は偽になり、それと同時に逆の命題も偽になります。
この時、「東大へ行くべき」⇒「バカまたはブス」と言う逆の命題も偽になるので、東大へ行けのポストは悪意を含まないことになります。
結論:阿部寛のいう通りにバカとブスこそ東大へ行くべきであったとしても、「東大へ行け」という投稿はあなたはブスまたはバカであるという悪意を含まない可能性があります。
次回予告 「バカとブスこそ東大へ行け」の構文で学ぶ係結びの法則 結びの省略と命令形
ぞ・なむ・や・か を古文では係助詞と呼びます。バカとブスこそ東大へ行け、のぶんの「こそ」を係助詞と考えて、行けが已然形で結ばれていると考えることができる気がしました。
これを題材に係結びの法則を考えてみたいと思います。
定期テストの勉強や受験勉強を東大生が教えてくれる
超高難度な東大入試に合格した現役東大生が持つ「戦略」と「実行」の勉強法
あなただけの勉強を提案してくれます!
完全オンラインだから他社の家庭教師より値段が安くて、それなのに合格率88% 定期テストで22.5UPの圧倒的実績
集合と命題だけでなく、定期テストでわからない場所を東大生に教えてもらえます!
無料体験、学習相談はこちらから⤵︎



コメント