現役東大生で、大手受験指導塾で算数講師をしています。
今回は、5年生が受験指導塾でならう流水算の中から、難しめの問題を紹介します。
難しいですが、流水算をしっかりと理解していれば、一瞬で解くことができて理解の差が現れるような問題です。
ぜひお子さんに解いてもらってみてください。
時計算が苦手なお子さんなら、ぜひ時計算の記事を読んでください
問題
問題
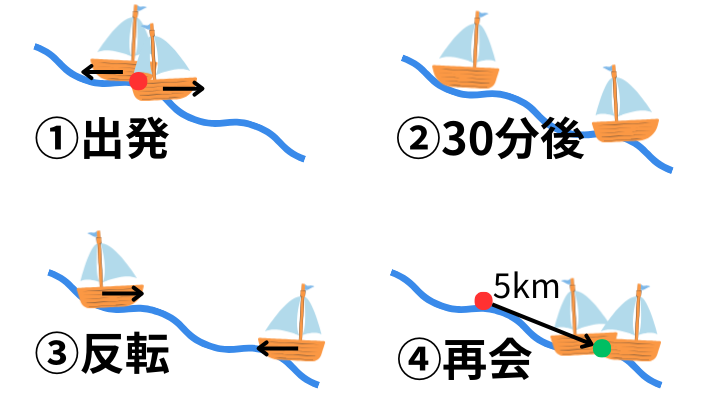
ある川で、静水時の速さが同じ2隻の船があります。
同じ地点から出発して、一方は上流に向かって、もう一方は下流に向かって30分進み、2隻とも、反転して向かい合う方向に進みました。
2隻の船が再び出会ったのは、出発地点から5km離れていました。流速を求めなさい。
まず、問題の意味が分かりにくいですね。図にすると以下のようになります。
答え
静水時の速さもわからなくて、上流で再会したのか下流で再会したのかもわからなくて、何時間後に再会したのかもわからなくて、わからないことずくめですね。
それでも理解していると一瞬で解くことができます。
ズバリ答えは流速5km/hです。
アテ勘でなく、きちんと理由を説明できますか? 解説していきます。
回りくどく解説する
最初に、問題がカンタに見える考え方をしないで、普通に解くとしたらどう解くかを見てもらおうと思います。
船の静水時の速さをV、流速をRとでもすると、上流に進み始めた船はV-Rで、下流に進み始めた船はV+Rで移動します。
30分後までに、{(V-R)+(V+R)}×1/2=2V×1/2=V 離れています。
その後2隻が反転して、下流に向かう船はV+Rで、上流に向かう船はV-Rで移動するので、V離れている状態から再会するまでには、
V÷{(V+R)+(V-R)}=V÷2V=1/2
つまり、反転してから、再会するまでには30分かかります。
最初に上流に向かって進み出した船について考えると、
上流に向かってV-Rで30分、下流に向かってV+Rで30分移動しているから、
合計で下流にRだけ移動しています。出発から再開までに合計で1時間かかっていますから1時間でV移動しました。
問題文に、5km離れていたとありますから、流速Rは5km/hだとわかります。
問題が解けたところで、注目に値する事実は
- 出発から反転、反転から再会までの時間が30分で同じ
- 出発地点から再会地点はRだけ移動していて、Vは関係ない
これは、言われてみると気づくという程度のことかもしれません。
しかし、ある考え方をすると、当たり前に感じられて、一瞬で問題を解くことができます。
簡単に見える考え方で解説する
次に、問題が簡単に見える考え方を紹介します。
その考え方とは、川にカメラを浮かべて流す、です。
何を言っているのか分からないかもしれませんが、文字通りに川にカメラを浮かべて流してみてください(頭の中で)
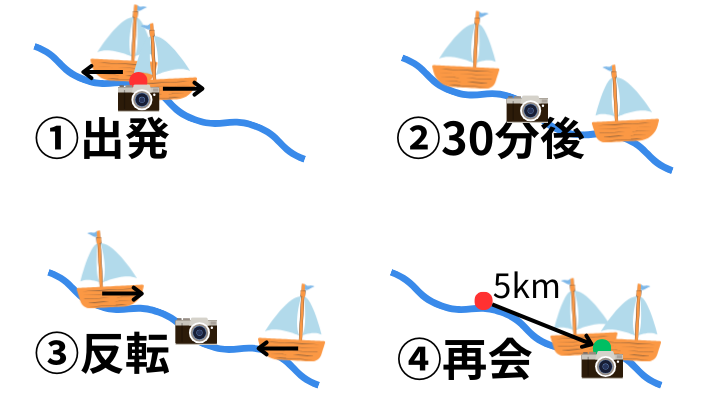
そのカメラからは2隻の船はどう見えるでしょうか。
2隻の船は同じ速さで二方向に離れていって、同じ速さで戻ってくるように見えます。
理由は、静水時の速さというのは、水に対しての速さという意味で、流水に対しての速さでもあるからです。
浮かべたカメラは、流れる水と一緒に移動します。流れる水に対してVの速さで移動する船は、カメラから見るともちろんVの速さで移動して見えます。
30分間Vで移動した分だけの距離から反転して近づいてくると、流れているカメラとすれ違うまでに、30分Vで移動すればいいです。
上流に向かった船と下流に向かった船の両方が、30分後に浮かんでるカメラとすれ違いますから、2隻の船が再会するのは、反転してから30分後で、浮かんでるカメラの位置です。
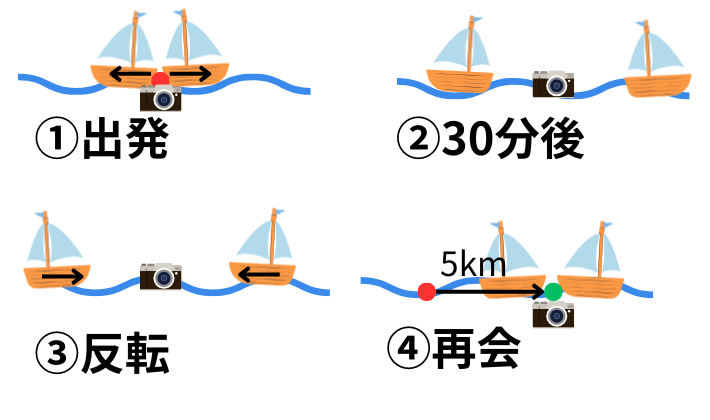
つまり、この問題を流れるカメラから見ると、2隻の船が30分間Vの速さで離れていって、30分間Vの速さで近づいてくるという問題です。
2隻の船が再会するまでの1時間、カメラは流れる水と一緒に流速で移動していますから、5km離れた位置で再会したのなら、流速は5km/hです。
このような考え方は、突拍子なく感じられますが、物理を重心系を勉強すると、こんな考え方があります。
陸から見た速さだとわからないことばかりで複雑に感じられれますが、水と一緒に移動する視点から見ると、問題は一気にシンプルになります。
- 出発から反転、反転から再会までの時間が30分で同じ
- 出発地点から再会地点はRだけ移動していて、Vは関係ない
先ほど確認した二つの事実も当たり前に見えませんか?
集団塾で理解が追いつくか不安な時は
集団塾は、大人数で授業を受けるという特性上、理解できていない生徒に合わせるということは難しいです。
一人一人に丁寧に指導するのには限度があります。
お子さんが授業についていけるか不安なら、家庭教師を検討してみるのも手の一つです。
現役東大生による家庭教師サービス『トウコべ』なら、まずは無料で面談できます。
自分で計画を立てて難関な受験を乗り越えた東大生が、生徒一人ひとりに合わせて勉強計画や勉強法を提案してくれます。


コメント