時計算を解説します。
私は現役東大生で、大手受験指導塾で算数の講師をしています。
今回は、時計算の中から
①長針と短針が重なる ②長針と短針が線対称(左右対称)になる
の2パターンの解き方やコツをわかりやすく解説をしていきます。
角度の変化を捉えて、長針と短針の間の角度の変化を掴み、旅人算的に考えるのが時計算の基本的な解き方です。
先に結論
手っ取り早く結論から言うと
針が重なる時の問題は、進んだ角度の差が大事で分母が11
線対称になる時の問題は進んだ角度の和が大事で分母が13
まだなんのことだかわからないかもしれませんが、記事の中でわかりやすくかつ細かく解説してきます。
【重要】長針と短針の1分間に進む角度
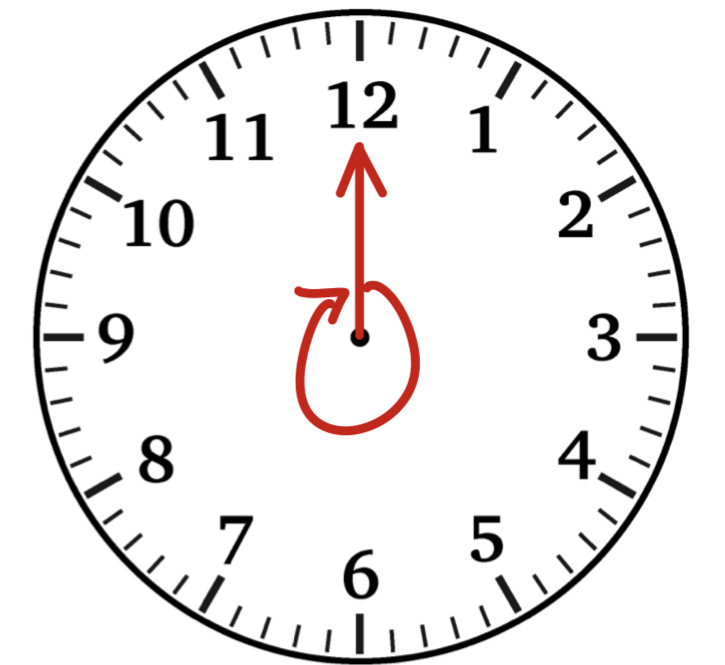
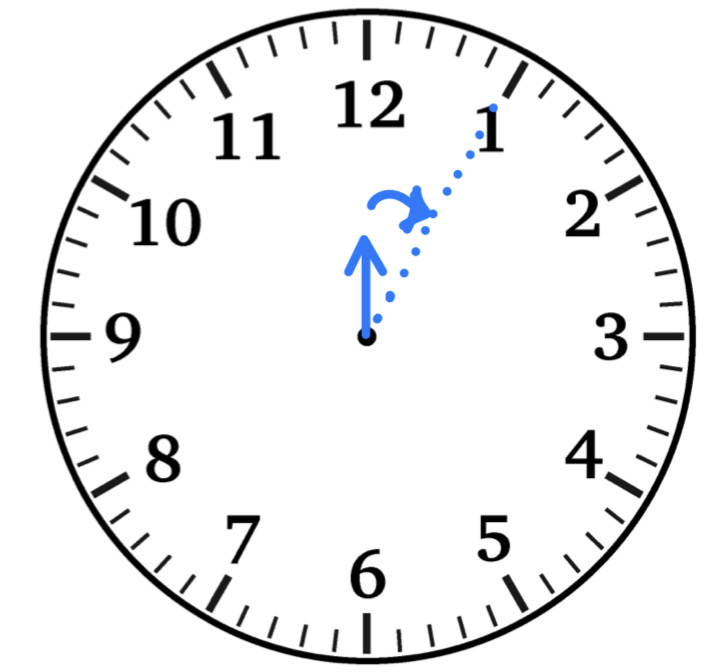
長針は1時間(60分)に一周(360°)するので、長針の1分間に動く角度は
360°÷60m=6[°/m]
短針は1時間(60分)に1目盛り分(30°)動くので、短針が1分間に動く角度は
30°÷60m=0.5[°/m]
長針と短針の進むスピードは時計算を解く時にとても重要で、この記事内でも何度も使います。覚えてしまってもいいです。
パターン① 長針と短針が重なる
問題 3時から4時の間で長針と短針が重なるのは何分ですか?
Ⅰ キリのいい時刻からの角度の変化を考える
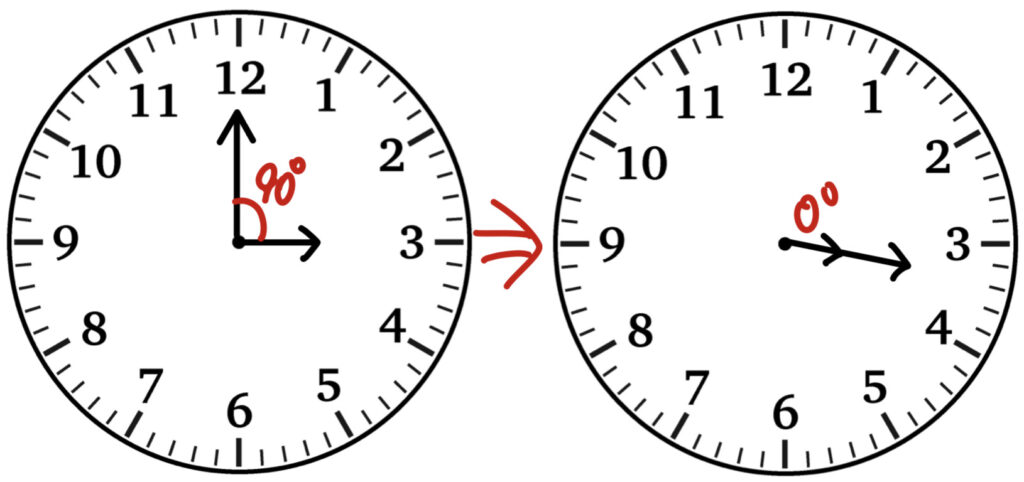
この問題ではキリのいい時間として、3時00分からの角度の変化を考えます。
3時から長針と短針が重なる時刻までの間に、長針と短針の間の角度が90°→0°へと変化しています。
Ⅱ 1分間に長針と短針の間の角度はどれくらい小さくなるか
長針は1分に6°、短針は1分に0.5°ずつ進むから、長針と短針の間の角度は1分に5.5°ずつ小さくなります。
1分に5.5°ずつ小さくなるのだから、90°小さくなるのにかかる時間は、
90[°]÷5.5[°/m]=90÷11/2[m]
=90×2/11[m]
=180/11[m]
=16+4/11[m]
3時00分から16+4/11分経った時刻に長針と短針が重なります。
分母が11になっているのがこの問題の特徴です。
Ⅲ 答えは妥当なのか
3時〜4時の間、短針は3と4の間にありますから、長針と短針が重なる時には長針も3と4の間にあります。
そうすると重なる時刻は、3時15分〜3時20分の間にあります。
計算して出た 3時16+4/11分 も、3時15分〜3時20分の間にあるから、答えとして妥当と言えます。
仮に、3時15分〜3時20分の間にない答えが出たとしたら、自分が計算ミスしていることに気づけます。
パターン② 長針と短針が線対称になる(◯時の方向が2等分する)
問題 10時から11時の間で長針と短針が時計の中心と12の目盛りを結ぶ直線に関して線対称になるのは何分ですか?
Ⅰ キリのいい時刻からの角度の変化を考える
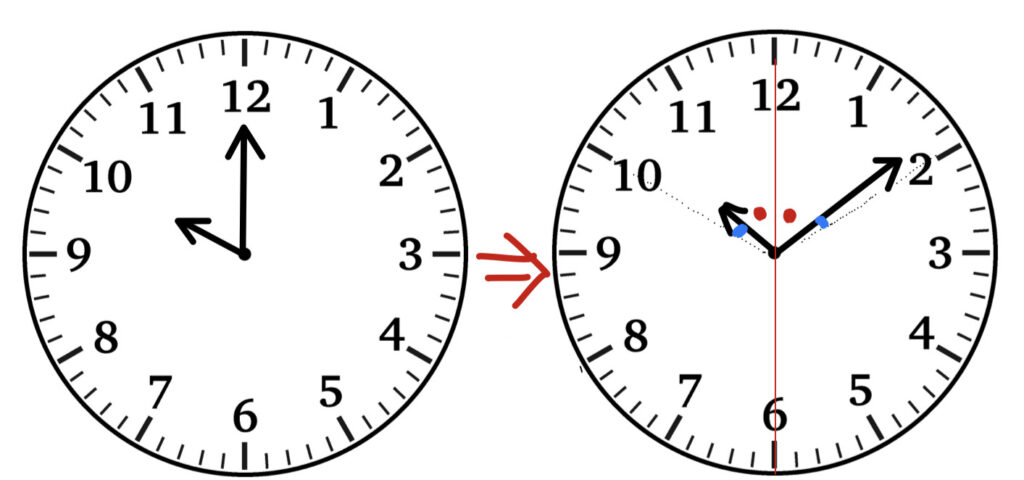
この問題ではキリのいい時刻として10時00分からの角度の変化を考えます。
10時00分から求める時刻までの間に、長針の進んだ角度の大きさが右側の赤い印です。12時の線に関して線対称ですから、左側にも赤い印をつけることができます。
10時00分から求める時刻までの間に、短針の進んだ角度の大きさが左側の青い印です。12時の線に関して線対称ですから、右側にも赤い印をつけることができます。
ここで、赤い印と青い印の角度の合計を考えます。すると、合計が2目盛り分で60°になっています。
長針と短針の進んだ角度の合計が60°になる時刻が、長針と短針が12の線に関して線対象になる時刻です。
Ⅱ 1分間に長針と短針は合計でどれくらい動くか
長針は1分に6°、短針は1分に0.5°ずつ進むから、長針と短針は1分間に合計で6.5°動きます。
10時00分から考えて、長針と短針が合計で60°動くときに針が線対称になるので
60[°]÷6.5[°/m]=60÷13/2[m]
=60×2/13[m]
=120/13[m]
=9+3/13[m]
10時00分から9+3/13分たったtきに長針と短針は12時の方向に関して線対称になります。
分母が13になっているのがこの問題の特徴です。
Ⅲ 答えは妥当なのか
10時から11時の間に、短針は10と11の目盛りの間にあります。
そうすると、線対称な位置に長針がくる時、長針は1と2のメモリに間にあるので、線対称な位置になる時刻は10時05分から10時10分の間です。
計算して出た 10時9+3/13分 も、3時15分〜3時20分の間にあるから、答えとして妥当と言えます。
仮に、10時05分から10時10分の間にない答えが出たとしたら、自分が計算ミスしていることに気づけます。
Ⅳ 12時以外の方向に関して線対称なとき
上で解説したのは12時の方向に関して線対称なときでした。
ただ12時以外の方向の時もあります。
そんな時も線対称を確実に捉えて、補助線を引きながら同じ角度のところに着目して、長針と短針の動く角度の合計を考えましょう。
まとめ
時計算の中から、針が重なる時、針が線対称になる時の解説をしました。
針が重なる時の問題は、長針と短針の進んだ角度の差が大事で、6-0.5=5.5が出てくる関係で、分母が11になります。
針が線対称になるときの問題は、長針と短針の進んだ角度の和が大事で、6+0.5=6.5が出てくる関係で、分母が13になります。
子供の理解のための確認事項
- 長針と短針の1分間に進む角度を理解できているか
- 線対称の時、補助線を引いて同じ角度を見つけれるか
- 旅人算(同じ方向に進んで追いつく 違う方向に進んで離れる)を理解できているか
集団塾で理解が追いつくか不安な時は
集団塾は、大人数で授業を受けるという特性上、理解できていない生徒に合わせるということは難しいです。
一人一人に丁寧に指導するのには限度があります。
お子さんが授業についていけるか不安なら、家庭教師を検討してみるのも手の一つです。
現役東大生による家庭教師サービス『トウコべ』なら、まずは無料で面談できます。
自分で計画を立てて難関な受験を乗り越えた東大生が、生徒一人ひとりに合わせて勉強計画や勉強法を提案してくれます。



コメント